23.11.2024 Redakcia Vášeň v tebe (Foto: súkromný archív).
Ste pripravení otestovať svoje matematické a logické schopnosti? Táto úloha nie je len tak pre každého – vyžaduje trpezlivosť, systematický prístup a schopnosť kombinovať základné vedomosti s logickým uvažovaním. Ak si myslíte, že na to máte, pustite sa do riešenia!
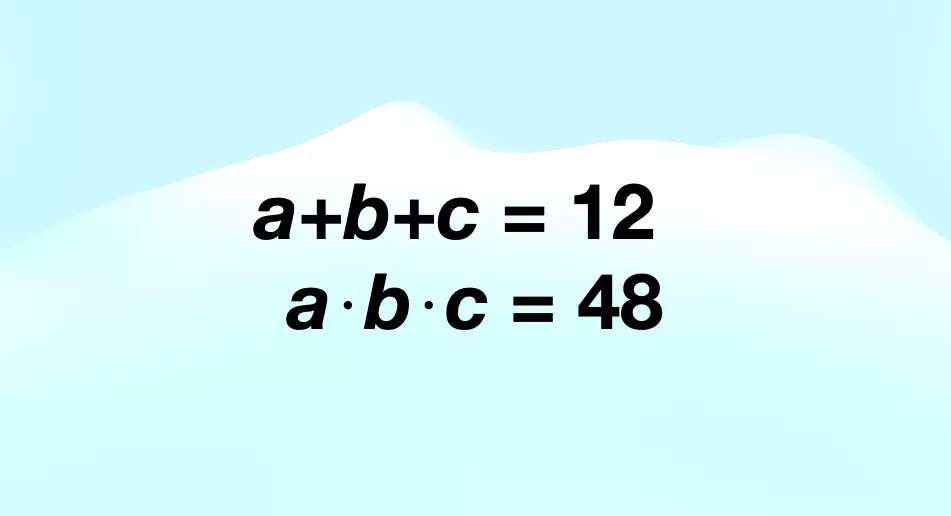
Foto: súkromný archív
Matematika nás sprevádza na každom kroku, od bežných výpočtov až po zložité problémy, ktoré lákajú tých najšikovnejších z nás. Aj jednoduché zadanie môže skrývať náročnosť, ktorá preverí logiku, trpezlivosť a schopnosť pracovať systematicky. Preto sme pre vás pripravili hádanku, ktorá na prvý pohľad vyzerá jednoducho, no len málokto ju vyrieši bez zaváhania. Pustite sa do toho a ukážte, čo vo vás je!
Zadanie: Máme tri čísla a, b a c, ktoré sú kladné celé čísla. Vieme, že:
- a+b+c = 12
- a⋅b⋅c = 48
Vašou úlohou je nájsť čísla a, b a c, ktoré spĺňajú obe tieto podmienky. Dokážete to?
Teraz sa pozrime na riešenie krok po kroku, aby sme pochopili, ako na to.
Krok 1: Práca s podmienkou a+b+c = 12
Vieme, že súčet troch čísel je 12. Preto môžeme skúšať rôzne hodnoty a, pričom platí b+c = 12−a. Tieto hodnoty musia byť celé čísla väčšie ako 0.
Pre jednoduchosť budeme skúšať jednotlivé hodnoty a a pre každú hodnotu hľadať také b a c, aby platili obe podmienky.
Krok 2: Skúšanie konkrétnych hodnôt a
Pre a = 2:
Ak a = 2, potom:
- b+c = 12−2 = 10
- Zároveň musí platiť b⋅c = 48
Hľadáme také dvojice b a c, ktoré dávajú súčet 10 a súčin 48:
- b = 4, c = 6: Súčet 4+6 = 10 a súčin 4⋅6 = 48. Platí!
- b = 6, c = 4: Súčet 6+4 = 10 a súčin 6⋅4 = 48. Platí!
Teda jedna možná trojica je: (a,b,c) = (2,4,6).
Pre a = 3:
Ak a = 3, potom:
- b + c = 12−3 = 9.
- Zároveň musí platiť b⋅c = 48.
Hľadáme dvojice b a c, ktoré dávajú súčet 9 a súčin 48:
- b = 3, c = 6: Súčin 3⋅6 = 18 (neplatí).
- b = 4, c = 5: Súčin 4⋅5 = 20 (neplatí).
Pre a = 3 neexistujú žiadne riešenia.
Pre a = 4:
Ak a = 4, potom:
- b+c = 12−4 = 8.
- Zároveň musí platiť b⋅c = 48.
Hľadáme dvojice b a c, ktoré dávajú súčet 8 a súčin 48:
- b = 2, c = 6: Súčin 2⋅6 = 12 (neplatí).
- b = 4, c = 4: Súčin 4⋅4=16 (neplatí).
Pre a = 4 neexistujú žiadne riešenia.
Krok 3: Záver
Jediné riešenie, ktoré spĺňa obe podmienky, je: (a,b,c) = (2,4,6).
Poradie čísel môže byť ľubovoľné, takže ďalšie možnosti sú: (2,6,4),(4,2,6),(4,6,2),(6,2,4),(6,4,2).
Čo na to hovoríte?
Táto hádanka preverí vaše logické schopnosti a vyžaduje systematický prístup. Ak ste to vyriešili sami, gratulujeme – patríte medzi šikovných! Máte chuť na ďalšiu výzvu?
Zaujímavosť zo sveta matematiky: Dokonalé čísla

Foto: súkromný archív
V matematike existujú tzv. dokonalé čísla – to sú čísla, ktoré sa rovnajú súčtu všetkých svojich deliteľov okrem seba. Napríklad číslo 6 je dokonalé, pretože jeho delitele sú 1, 2 a 3 a platí:1+2+3=6.
Ďalším dokonalým číslom je 28, pretože 1+2+4+7+14=28. Zaujímavosťou je, že všetky známe dokonalé čísla súvisia s tzv. Mersennovými prvočíslami, čo sú prvočísla tvaru 2p−1, kde p je tiež prvočíslo.
Súvisiace články:
Matematická výzva: Koľko je 6 deleno polovicou? Odpoveď vás môže prekvapiť!
Máte IQ vyššie ako 110? Táto logická hádanka preverí váš dôvtip!
Matematický hlavolam: pravdepodobnosť a stratégia. Ako prežiť v matematickej prestrelke?
Boli ste najlepší v matematike? Potom je pre vás táto úloha hračkou
Ďakujeme, že ste si prečítali náš článok. Odporúčame vám sledovať nás v službe Google News.