27.11.2024 Redakcia Vášeň v tebe (Foto: súkromný archív).
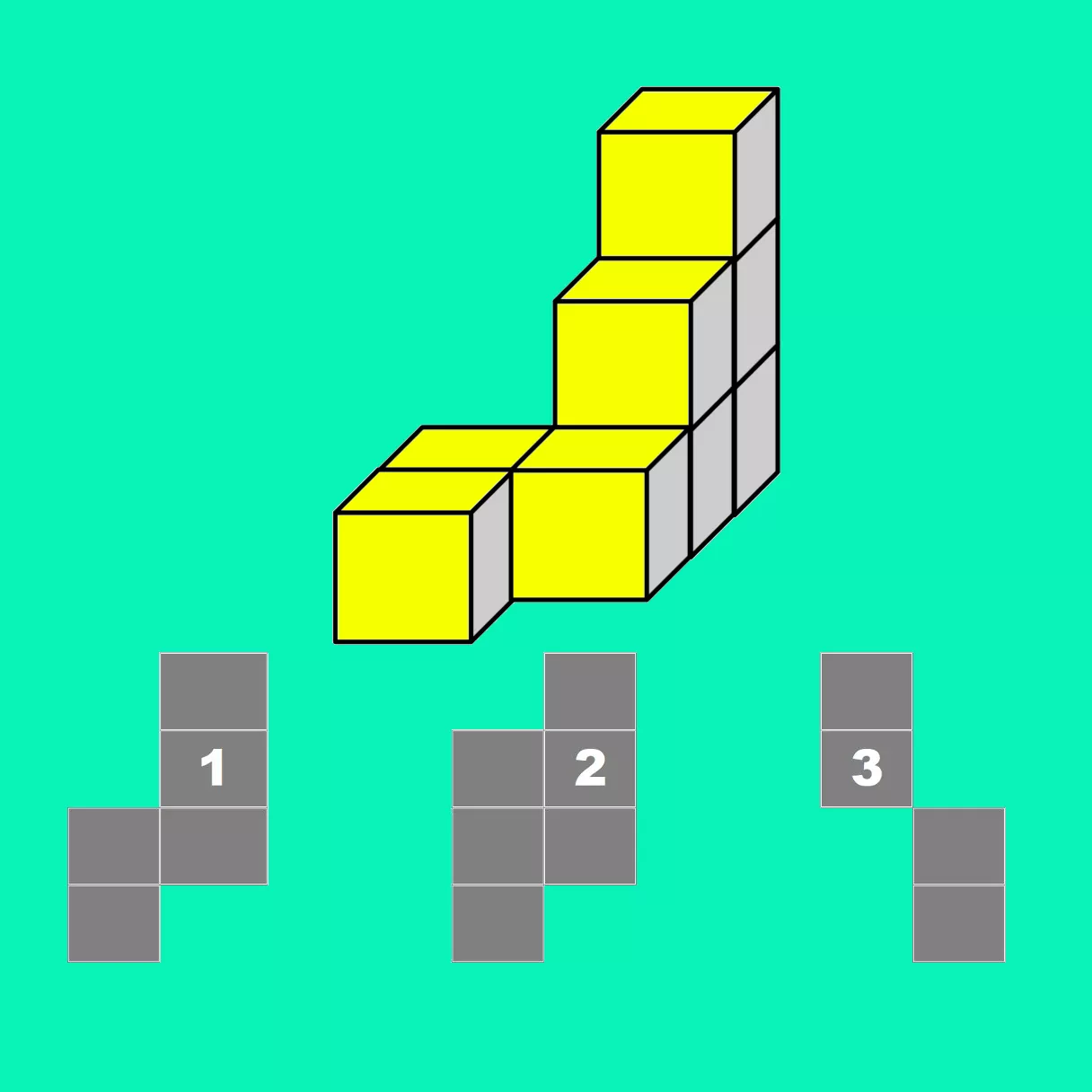
Matematika dokáže byť nielen náročná, ale aj fascinujúca. Dnešná hádanka preverí vaše logické myslenie a schopnosť hľadať vzory. Predstavte si sedem schodov, po ktorých sa môžete pohybovať len smerom nahor – buď po jednom schode, alebo preskočiť rovno na druhý. Koľkými rôznymi spôsobmi sa dá dostať na posledný schod? Ide o kombinatorický problém, ktorý poteší každého milovníka matematiky a logiky!

Foto: súkromný archív
Matematika nás obklopuje na každom kroku, od jednoduchých rozhodnutí až po najzložitejšie problémy, ktoré ovplyvňujú náš svet. Dnešná hádanka je zábavným príkladom toho, ako sa dá matematika prepojiť s každodenným životom. Schody, po ktorých sa musíme dostať na vrchol, symbolizujú naše možnosti a výpočty ukazujú, ako môžeme efektívne hľadať riešenia.
Táto úloha nie je len o počítaní – ide o schopnosť pochopiť vzory a princípy, ktoré sa skrývajú za obyčajnými číslami. Fibonacciho čísla, ktoré zohrávajú kľúčovú úlohu v tomto probléme, sú jedným z najznámejších matematických konceptov, ktoré nachádzajú svoje využitie nielen v matematike, ale aj v prírode, umení a technológiách.
Vyriešte túto matematickú lahôdku a objavte kúzlo logiky ukryté v jednoduchých schodoch!
- Na vyvýšené prízemie vedie sedem schodov. Sú tak ďaleko od seba, že je možné vystúpiť na ďalší schod alebo prekročiť jeden schod a urobiť dva. Koľkými rôznymi spôsobmi sa môžeme dostať z prízemia na posledný schod, ak smieme ísť len hore a nikdy nie dole?
Tento hlavolam je klasickým príkladom kombinatorického problému, ktorý je úzko spojený s Fibonacciho číslami. Každý spôsob, ako sa dostať na posledný schod, závisí od toho, ako ste sa dostali na predposledný alebo predpredposledný schod.
Kľúčová idea
- Ak stojíte na poslednom (7.) schode, mohli ste tam prísť buď:
- Zo 6. schodu (krok o 1 schod).
- Z 5. schodu (krok o 2 schody).
Z tohto vyplýva, že počet spôsobov, ako sa dostať na 7. schod, je súčtom počtu spôsobov, ako sa dostať na 6. a 5. schod:
f(7) = f(6) + f(5)
Tento vzťah je typický pre Fibonacciho postupnosť:
f(n) = f(n−1) + f(n−2)
Základné prípady
- Ak je n = 1 (iba prvý schod): Je len jeden spôsob, ako tam vystúpiť – jedným krokom.
f(1) = 1 - Ak je n = 2 (druhý schod): Sú dva spôsoby – buď dvakrát po jednom schode, alebo jedným krokom preskočiť na druhý schod.
f(2) = 2
Výpočet
Teraz postupne vypočítame počet spôsobov pre všetky schody až po 7:
f(3) = f(2) + f(1) = 2 + 1 = 3
f(4) = f(3) + f(2) = 3 + 2 = 5
f(5) = f(4) + f(3) = 5 + 3 = 8
f(6) = f(5) + f(4) = 8+5 = 13
f(7) = f(6) + f(5 )= 13+8 = 21
Odpoveď
Na posledný (7.) schod sa môžeme dostať 21 rôznymi spôsobmi.
Prečo Fibonacciho čísla?

Foto: shutterstock/Framarzo
Tento problém využíva Fibonacciho čísla, pretože každý krok závisí od dvoch predchádzajúcich možností. Podobné problémy sa často objavujú pri riešení otázok o ceste alebo pohybe, kde existujú obmedzené kroky alebo možnosti.
Redakcia Vášeň v tebe.
Súvisiace články:
Máte IQ vyššie ako 110? Táto logická hádanka preverí váš dôvtip!
Ďakujeme, že ste si prečítali náš článok. Odporúčame vám sledovať nás v službe Google News.